Note
Click here to download the full example code
Coordinate-based meta-analysis algorithms
A tour of CBMA algorithms in NiMARE.
This tutorial is intended to provide a brief description and example of each of the CBMA algorithms implemented in NiMARE. For a more detailed introduction to the elements of a coordinate-based meta-analysis, see other stuff.
Load Dataset
Note
The data used in this example come from a collection of NIDM-Results packs downloaded from Neurovault collection 1425, uploaded by Dr. Camille Maumet.
Creation of the Dataset from the NIDM-Results packs was done with custom code. The Results packs for collection 1425 are not completely NIDM-Results-compliant, so the nidmresults library could not be used to facilitate data extraction.
import os
from nilearn.plotting import plot_stat_map
from nimare.correct import FWECorrector
from nimare.dataset import Dataset
from nimare.utils import get_resource_path
dset_file = os.path.join(get_resource_path(), "nidm_pain_dset.json")
dset = Dataset(dset_file)
# Some of the CBMA algorithms compare two Datasets,
# so we'll split this example Dataset in half.
dset1 = dset.slice(dset.ids[:10])
dset2 = dset.slice(dset.ids[10:])
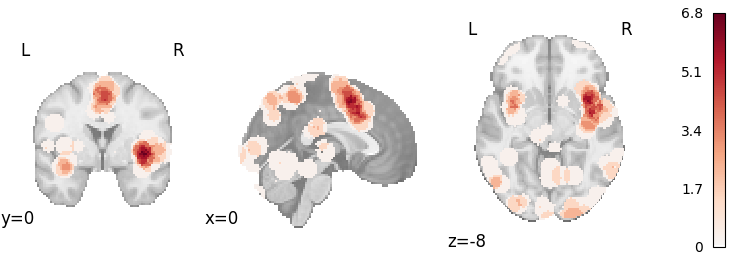
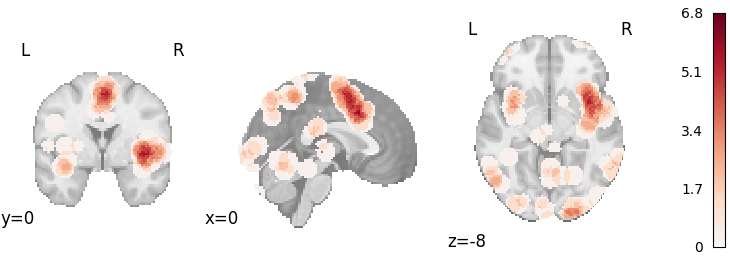
Multilevel Kernel Density Analysis
from nimare.meta.cbma.mkda import MKDADensity
meta = MKDADensity()
results = meta.fit(dset)
corr = FWECorrector(method="montecarlo", n_iters=10, n_cores=1)
cres = corr.transform(results)
plot_stat_map(
results.get_map("z"),
cut_coords=[0, 0, -8],
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
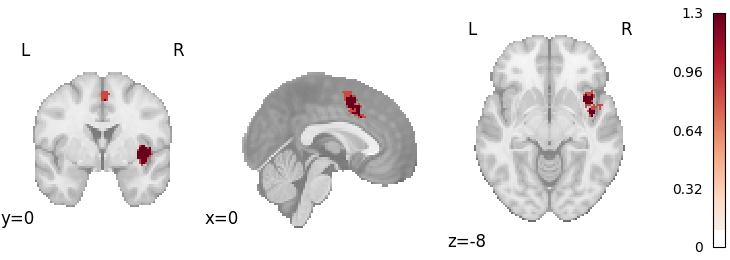
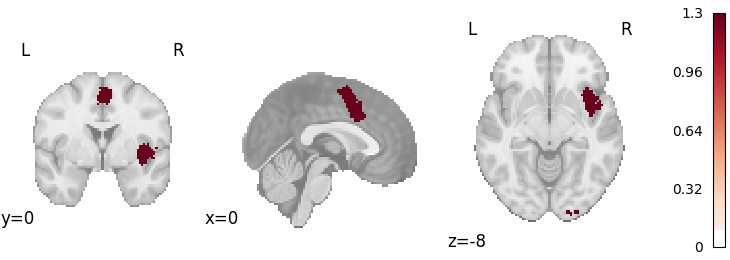
plot_stat_map(
cres.get_map("z_level-voxel_corr-FWE_method-montecarlo"),
cut_coords=[0, 0, -8],
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
Out:
0%| | 0/10 [00:00<?, ?it/s]
10%|# | 1/10 [00:00<00:03, 2.70it/s]
20%|## | 2/10 [00:00<00:02, 2.76it/s]
30%|### | 3/10 [00:01<00:02, 2.76it/s]
40%|#### | 4/10 [00:01<00:02, 2.78it/s]
50%|##### | 5/10 [00:01<00:01, 2.77it/s]
60%|###### | 6/10 [00:02<00:01, 2.78it/s]
70%|####### | 7/10 [00:02<00:01, 2.77it/s]
80%|######## | 8/10 [00:02<00:00, 2.77it/s]
90%|######### | 9/10 [00:03<00:00, 2.77it/s]
100%|##########| 10/10 [00:03<00:00, 2.77it/s]
100%|##########| 10/10 [00:03<00:00, 2.77it/s]
<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f59f69b46d0>
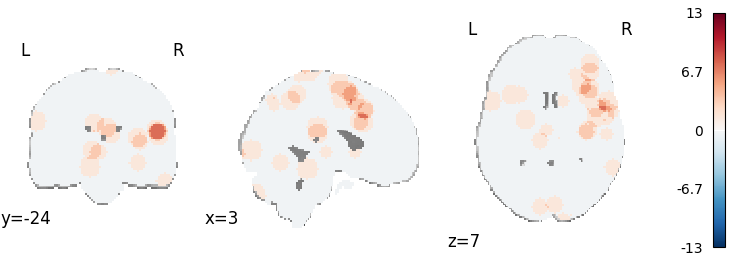
MKDA Chi-Squared
from nimare.meta.cbma.mkda import MKDAChi2
meta = MKDAChi2(kernel__r=10)
results = meta.fit(dset1, dset2)
corr = FWECorrector(method="montecarlo", n_iters=10, n_cores=1)
cres = corr.transform(results)
plot_stat_map(
results.get_map("z_desc-consistency"),
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
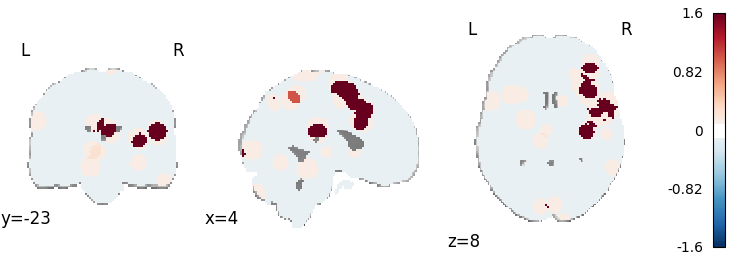
plot_stat_map(
cres.get_map("z_desc-consistencySize_level-cluster_corr-FWE_method-montecarlo"),
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
Out:
/home/docs/checkouts/readthedocs.org/user_builds/nimare/checkouts/744/nimare/meta/cbma/mkda.py:392: RuntimeWarning: invalid value encountered in true_divide
pFgA = pAgF * pF / pA
/home/docs/checkouts/readthedocs.org/user_builds/nimare/checkouts/744/nimare/meta/cbma/mkda.py:398: RuntimeWarning: invalid value encountered in true_divide
pFgA_prior = pAgF * self.prior / pAgF_prior
0%| | 0/10 [00:00<?, ?it/s]
10%|# | 1/10 [00:00<00:06, 1.45it/s]
20%|## | 2/10 [00:01<00:05, 1.47it/s]
30%|### | 3/10 [00:02<00:04, 1.46it/s]
40%|#### | 4/10 [00:02<00:04, 1.46it/s]
50%|##### | 5/10 [00:03<00:03, 1.46it/s]
60%|###### | 6/10 [00:04<00:02, 1.46it/s]
70%|####### | 7/10 [00:04<00:02, 1.47it/s]
80%|######## | 8/10 [00:05<00:01, 1.47it/s]
90%|######### | 9/10 [00:06<00:00, 1.47it/s]
100%|##########| 10/10 [00:06<00:00, 1.47it/s]
100%|##########| 10/10 [00:06<00:00, 1.47it/s]
<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f59f663bad0>
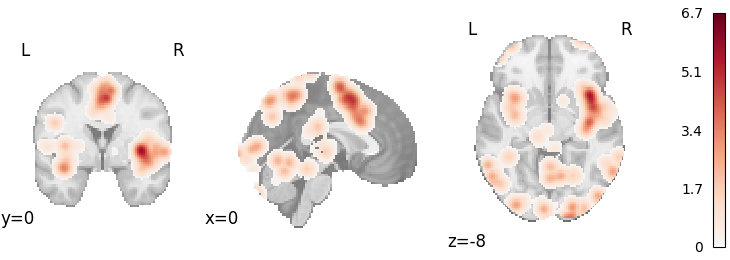
Kernel Density Analysis
from nimare.meta.cbma.mkda import KDA
meta = KDA()
results = meta.fit(dset)
corr = FWECorrector(method="montecarlo", n_iters=10, n_cores=1)
cres = corr.transform(results)
plot_stat_map(
results.get_map("z"),
cut_coords=[0, 0, -8],
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
plot_stat_map(
cres.get_map("z_desc-size_level-cluster_corr-FWE_method-montecarlo"),
cut_coords=[0, 0, -8],
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
Out:
0%| | 0/10 [00:00<?, ?it/s]
10%|# | 1/10 [00:00<00:03, 2.66it/s]
20%|## | 2/10 [00:00<00:02, 2.72it/s]
30%|### | 3/10 [00:01<00:02, 2.72it/s]
40%|#### | 4/10 [00:01<00:02, 2.71it/s]
50%|##### | 5/10 [00:01<00:01, 2.72it/s]
60%|###### | 6/10 [00:02<00:01, 2.69it/s]
70%|####### | 7/10 [00:02<00:01, 2.70it/s]
80%|######## | 8/10 [00:02<00:00, 2.71it/s]
90%|######### | 9/10 [00:03<00:00, 2.71it/s]
100%|##########| 10/10 [00:03<00:00, 2.71it/s]
100%|##########| 10/10 [00:03<00:00, 2.71it/s]
<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f59f65b37d0>
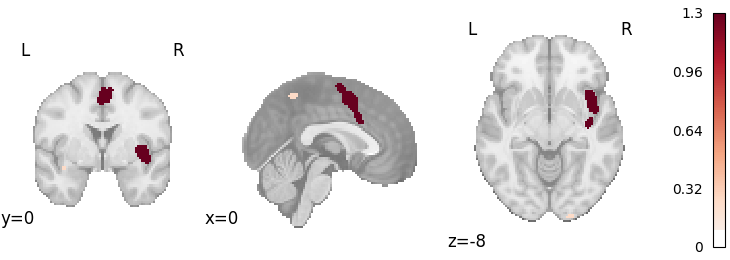
Activation Likelihood Estimation
from nimare.meta.cbma.ale import ALE
meta = ALE()
results = meta.fit(dset)
corr = FWECorrector(method="montecarlo", n_iters=10, n_cores=1)
cres = corr.transform(results)
plot_stat_map(
results.get_map("z"),
cut_coords=[0, 0, -8],
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
plot_stat_map(
cres.get_map("z_desc-size_level-cluster_corr-FWE_method-montecarlo"),
cut_coords=[0, 0, -8],
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
Out:
0%| | 0/10 [00:00<?, ?it/s]
10%|# | 1/10 [00:00<00:05, 1.54it/s]
20%|## | 2/10 [00:01<00:05, 1.59it/s]
30%|### | 3/10 [00:01<00:04, 1.62it/s]
40%|#### | 4/10 [00:02<00:03, 1.63it/s]
50%|##### | 5/10 [00:03<00:03, 1.64it/s]
60%|###### | 6/10 [00:03<00:02, 1.64it/s]
70%|####### | 7/10 [00:04<00:01, 1.64it/s]
80%|######## | 8/10 [00:04<00:01, 1.64it/s]
90%|######### | 9/10 [00:05<00:00, 1.63it/s]
100%|##########| 10/10 [00:06<00:00, 1.62it/s]
100%|##########| 10/10 [00:06<00:00, 1.62it/s]
<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f59f696b490>
Specific Co-Activation Likelihood Estimation
Important
The SCALE algorithm is very memory intensive, so we don’t run it within the documentation.
ALE-Based Subtraction Analysis
from nimare.meta.cbma.ale import ALESubtraction
meta = ALESubtraction(n_iters=10, n_cores=1)
results = meta.fit(dset1, dset2)
plot_stat_map(
results.get_map("z_desc-group1MinusGroup2"),
cut_coords=[0, 0, -8],
draw_cross=False,
cmap="RdBu_r",
threshold=0.1,
)
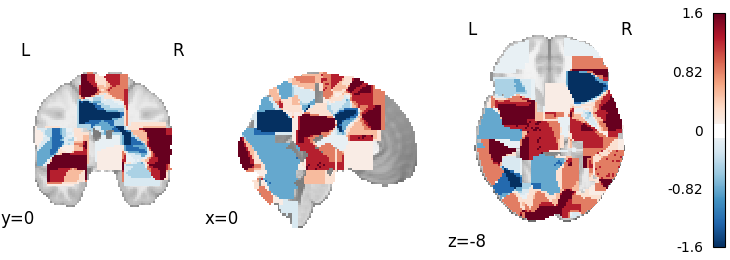
Out:
0%| | 0/10 [00:00<?, ?it/s]
10%|# | 1/10 [00:03<00:30, 3.33s/it]
20%|## | 2/10 [00:03<00:12, 1.50s/it]
30%|### | 3/10 [00:03<00:06, 1.09it/s]
40%|#### | 4/10 [00:04<00:03, 1.55it/s]
50%|##### | 5/10 [00:04<00:02, 2.03it/s]
60%|###### | 6/10 [00:04<00:01, 2.50it/s]
70%|####### | 7/10 [00:04<00:01, 2.92it/s]
80%|######## | 8/10 [00:04<00:00, 3.28it/s]
90%|######### | 9/10 [00:05<00:00, 3.60it/s]
100%|##########| 10/10 [00:05<00:00, 3.83it/s]
100%|##########| 10/10 [00:05<00:00, 1.87it/s]
0%| | 0/228483 [00:00<?, ?it/s]
0%| | 1099/228483 [00:00<00:20, 10989.51it/s]
1%| | 2198/228483 [00:00<00:20, 10982.24it/s]
1%|1 | 3297/228483 [00:00<00:20, 10964.66it/s]
2%|1 | 4394/228483 [00:00<00:20, 10959.88it/s]
2%|2 | 5490/228483 [00:00<00:20, 10923.46it/s]
3%|2 | 6610/228483 [00:00<00:20, 11015.75it/s]
3%|3 | 7712/228483 [00:00<00:20, 11011.55it/s]
4%|3 | 8817/228483 [00:00<00:19, 11021.29it/s]
4%|4 | 9924/228483 [00:00<00:19, 11034.39it/s]
5%|4 | 11028/228483 [00:01<00:19, 11018.13it/s]
5%|5 | 12138/228483 [00:01<00:19, 11041.70it/s]
6%|5 | 13257/228483 [00:01<00:19, 11084.16it/s]
6%|6 | 14372/228483 [00:01<00:19, 11101.43it/s]
7%|6 | 15486/228483 [00:01<00:19, 11112.37it/s]
7%|7 | 16598/228483 [00:01<00:19, 11109.58it/s]
8%|7 | 17709/228483 [00:01<00:19, 11074.89it/s]
8%|8 | 18817/228483 [00:01<00:18, 11068.73it/s]
9%|8 | 19944/228483 [00:01<00:18, 11127.26it/s]
9%|9 | 21057/228483 [00:01<00:18, 11086.29it/s]
10%|9 | 22166/228483 [00:02<00:18, 11083.52it/s]
10%|# | 23275/228483 [00:02<00:18, 11049.14it/s]
11%|# | 24380/228483 [00:02<00:18, 11012.52it/s]
11%|#1 | 25490/228483 [00:02<00:18, 11037.09it/s]
12%|#1 | 26594/228483 [00:02<00:26, 7619.15it/s]
12%|#2 | 27717/228483 [00:02<00:23, 8440.89it/s]
13%|#2 | 28812/228483 [00:02<00:22, 9055.04it/s]
13%|#3 | 29936/228483 [00:02<00:20, 9621.27it/s]
14%|#3 | 31054/228483 [00:02<00:19, 10041.05it/s]
14%|#4 | 32182/228483 [00:03<00:18, 10384.35it/s]
15%|#4 | 33307/228483 [00:03<00:18, 10628.22it/s]
15%|#5 | 34415/228483 [00:03<00:18, 10758.67it/s]
16%|#5 | 35543/228483 [00:03<00:17, 10909.52it/s]
16%|#6 | 36657/228483 [00:03<00:17, 10975.35it/s]
17%|#6 | 37767/228483 [00:03<00:17, 10988.88it/s]
17%|#7 | 38896/228483 [00:03<00:17, 11076.97it/s]
18%|#7 | 40019/228483 [00:03<00:16, 11120.11it/s]
18%|#8 | 41136/228483 [00:03<00:16, 11041.84it/s]
18%|#8 | 42244/228483 [00:03<00:16, 11036.63it/s]
19%|#8 | 43363/228483 [00:04<00:16, 11081.67it/s]
19%|#9 | 44479/228483 [00:04<00:16, 11103.47it/s]
20%|#9 | 45594/228483 [00:04<00:16, 11117.04it/s]
20%|## | 46709/228483 [00:04<00:16, 11124.71it/s]
21%|## | 47823/228483 [00:04<00:16, 11114.43it/s]
21%|##1 | 48935/228483 [00:04<00:16, 11094.45it/s]
22%|##1 | 50045/228483 [00:04<00:16, 10985.88it/s]
22%|##2 | 51144/228483 [00:04<00:17, 10285.84it/s]
23%|##2 | 52195/228483 [00:04<00:17, 10349.43it/s]
23%|##3 | 53237/228483 [00:04<00:17, 10212.17it/s]
24%|##3 | 54270/228483 [00:05<00:17, 10244.22it/s]
24%|##4 | 55324/228483 [00:05<00:16, 10330.37it/s]
25%|##4 | 56369/228483 [00:05<00:16, 10363.21it/s]
25%|##5 | 57427/228483 [00:05<00:16, 10423.44it/s]
26%|##5 | 58471/228483 [00:05<00:16, 10419.16it/s]
26%|##6 | 59523/228483 [00:05<00:16, 10448.78it/s]
27%|##6 | 60576/228483 [00:05<00:16, 10472.35it/s]
27%|##6 | 61631/228483 [00:05<00:15, 10494.18it/s]
27%|##7 | 62681/228483 [00:05<00:15, 10458.57it/s]
28%|##7 | 63736/228483 [00:05<00:15, 10485.77it/s]
28%|##8 | 64785/228483 [00:06<00:22, 7344.34it/s]
29%|##8 | 65900/228483 [00:06<00:19, 8220.62it/s]
29%|##9 | 66990/228483 [00:06<00:18, 8883.19it/s]
30%|##9 | 68094/228483 [00:06<00:16, 9445.03it/s]
30%|### | 69215/228483 [00:06<00:16, 9923.03it/s]
31%|### | 70319/228483 [00:06<00:15, 10234.85it/s]
31%|###1 | 71428/228483 [00:06<00:14, 10477.06it/s]
32%|###1 | 72522/228483 [00:06<00:14, 10608.92it/s]
32%|###2 | 73644/228483 [00:07<00:14, 10785.64it/s]
33%|###2 | 74741/228483 [00:07<00:14, 10839.84it/s]
33%|###3 | 75848/228483 [00:07<00:13, 10905.39it/s]
34%|###3 | 76973/228483 [00:07<00:13, 11005.05it/s]
34%|###4 | 78102/228483 [00:07<00:13, 11089.47it/s]
35%|###4 | 79215/228483 [00:07<00:13, 11020.04it/s]
35%|###5 | 80329/228483 [00:07<00:13, 11054.34it/s]
36%|###5 | 81442/228483 [00:07<00:13, 11074.95it/s]
36%|###6 | 82555/228483 [00:07<00:13, 11091.34it/s]
37%|###6 | 83666/228483 [00:07<00:13, 11094.14it/s]
37%|###7 | 84791/228483 [00:08<00:12, 11138.45it/s]
38%|###7 | 85910/228483 [00:08<00:12, 11152.61it/s]
38%|###8 | 87032/228483 [00:08<00:12, 11170.49it/s]
39%|###8 | 88150/228483 [00:08<00:12, 11130.58it/s]
39%|###9 | 89264/228483 [00:08<00:12, 11077.17it/s]
40%|###9 | 90372/228483 [00:08<00:12, 11061.71it/s]
40%|#### | 91479/228483 [00:08<00:12, 11059.04it/s]
41%|#### | 92585/228483 [00:08<00:12, 11042.37it/s]
41%|####1 | 93690/228483 [00:08<00:12, 11036.39it/s]
41%|####1 | 94796/228483 [00:08<00:12, 11042.37it/s]
42%|####1 | 95901/228483 [00:09<00:12, 11040.01it/s]
42%|####2 | 97017/228483 [00:09<00:11, 11074.34it/s]
43%|####2 | 98136/228483 [00:09<00:11, 11107.48it/s]
43%|####3 | 99257/228483 [00:09<00:11, 11135.78it/s]
44%|####3 | 100371/228483 [00:09<00:11, 11065.61it/s]
44%|####4 | 101478/228483 [00:09<00:11, 11060.04it/s]
45%|####4 | 102611/228483 [00:09<00:11, 11137.70it/s]
45%|####5 | 103725/228483 [00:09<00:11, 11132.99it/s]
46%|####5 | 104839/228483 [00:09<00:11, 11126.83it/s]
46%|####6 | 105952/228483 [00:09<00:11, 11121.00it/s]
47%|####6 | 107074/228483 [00:10<00:10, 11149.86it/s]
47%|####7 | 108190/228483 [00:10<00:10, 11124.65it/s]
48%|####7 | 109314/228483 [00:10<00:10, 11158.86it/s]
48%|####8 | 110430/228483 [00:10<00:10, 11158.30it/s]
49%|####8 | 111546/228483 [00:10<00:10, 11122.15it/s]
49%|####9 | 112659/228483 [00:10<00:15, 7385.24it/s]
50%|####9 | 113749/228483 [00:10<00:14, 8160.67it/s]
50%|##### | 114852/228483 [00:10<00:12, 8848.20it/s]
51%|##### | 115975/228483 [00:11<00:11, 9455.51it/s]
51%|#####1 | 117077/228483 [00:11<00:11, 9872.91it/s]
52%|#####1 | 118179/228483 [00:11<00:10, 10188.50it/s]
52%|#####2 | 119282/228483 [00:11<00:10, 10425.73it/s]
53%|#####2 | 120405/228483 [00:11<00:10, 10654.70it/s]
53%|#####3 | 121509/228483 [00:11<00:09, 10765.07it/s]
54%|#####3 | 122630/228483 [00:11<00:09, 10893.76it/s]
54%|#####4 | 123754/228483 [00:11<00:09, 10993.72it/s]
55%|#####4 | 124877/228483 [00:11<00:09, 11061.61it/s]
55%|#####5 | 125991/228483 [00:11<00:09, 11070.68it/s]
56%|#####5 | 127103/228483 [00:12<00:09, 11057.71it/s]
56%|#####6 | 128224/228483 [00:12<00:09, 11100.50it/s]
57%|#####6 | 129347/228483 [00:12<00:08, 11137.70it/s]
57%|#####7 | 130463/228483 [00:12<00:08, 11132.49it/s]
58%|#####7 | 131578/228483 [00:12<00:08, 11028.60it/s]
58%|#####8 | 132682/228483 [00:12<00:08, 11015.11it/s]
59%|#####8 | 133796/228483 [00:12<00:08, 11051.07it/s]
59%|#####9 | 134902/228483 [00:12<00:08, 10986.93it/s]
60%|#####9 | 136002/228483 [00:12<00:08, 10990.75it/s]
60%|###### | 137122/228483 [00:12<00:08, 11050.95it/s]
60%|###### | 138228/228483 [00:13<00:08, 11032.28it/s]
61%|###### | 139332/228483 [00:13<00:08, 10951.08it/s]
61%|######1 | 140437/228483 [00:13<00:08, 10979.66it/s]
62%|######1 | 141550/228483 [00:13<00:07, 11021.98it/s]
62%|######2 | 142655/228483 [00:13<00:07, 11029.97it/s]
63%|######2 | 143759/228483 [00:13<00:07, 11020.45it/s]
63%|######3 | 144889/228483 [00:13<00:07, 11103.65it/s]
64%|######3 | 146000/228483 [00:13<00:07, 11092.30it/s]
64%|######4 | 147110/228483 [00:13<00:07, 10994.71it/s]
65%|######4 | 148210/228483 [00:13<00:07, 10794.55it/s]
65%|######5 | 149291/228483 [00:14<00:07, 10719.76it/s]
66%|######5 | 150364/228483 [00:14<00:07, 10643.54it/s]
66%|######6 | 151429/228483 [00:14<00:07, 10603.64it/s]
67%|######6 | 152490/228483 [00:14<00:07, 10557.61it/s]
67%|######7 | 153546/228483 [00:14<00:07, 10480.87it/s]
68%|######7 | 154595/228483 [00:14<00:07, 10448.45it/s]
68%|######8 | 155640/228483 [00:14<00:06, 10445.50it/s]
69%|######8 | 156685/228483 [00:14<00:06, 10444.36it/s]
69%|######9 | 157730/228483 [00:14<00:06, 10412.88it/s]
69%|######9 | 158778/228483 [00:14<00:06, 10431.61it/s]
70%|######9 | 159827/228483 [00:15<00:06, 10446.80it/s]
70%|####### | 160872/228483 [00:15<00:06, 10372.68it/s]
71%|####### | 161917/228483 [00:15<00:06, 10395.03it/s]
71%|#######1 | 162969/228483 [00:15<00:06, 10430.09it/s]
72%|#######1 | 164019/228483 [00:15<00:06, 10448.48it/s]
72%|#######2 | 165068/228483 [00:15<00:06, 10458.39it/s]
73%|#######2 | 166121/228483 [00:15<00:05, 10477.18it/s]
73%|#######3 | 167176/228483 [00:15<00:05, 10496.86it/s]
74%|#######3 | 168226/228483 [00:15<00:05, 10483.34it/s]
74%|#######4 | 169275/228483 [00:15<00:05, 10453.42it/s]
75%|#######4 | 170321/228483 [00:16<00:08, 6702.15it/s]
75%|#######5 | 171363/228483 [00:16<00:07, 7499.98it/s]
75%|#######5 | 172388/228483 [00:16<00:06, 8144.69it/s]
76%|#######5 | 173418/228483 [00:16<00:06, 8684.25it/s]
76%|#######6 | 174470/228483 [00:16<00:05, 9167.95it/s]
77%|#######6 | 175505/228483 [00:16<00:05, 9490.59it/s]
77%|#######7 | 176541/228483 [00:16<00:05, 9733.49it/s]
78%|#######7 | 177592/228483 [00:16<00:05, 9954.75it/s]
78%|#######8 | 178640/228483 [00:17<00:04, 10104.97it/s]
79%|#######8 | 179685/228483 [00:17<00:04, 10203.08it/s]
79%|#######9 | 180731/228483 [00:17<00:04, 10277.09it/s]
80%|#######9 | 181789/228483 [00:17<00:04, 10364.56it/s]
80%|######## | 182842/228483 [00:17<00:04, 10412.95it/s]
80%|######## | 183889/228483 [00:17<00:04, 10410.50it/s]
81%|######## | 184938/228483 [00:17<00:04, 10431.31it/s]
81%|########1 | 185993/228483 [00:17<00:04, 10464.45it/s]
82%|########1 | 187042/228483 [00:17<00:03, 10469.64it/s]
82%|########2 | 188091/228483 [00:17<00:03, 10461.14it/s]
83%|########2 | 189139/228483 [00:18<00:03, 10466.31it/s]
83%|########3 | 190188/228483 [00:18<00:03, 10471.80it/s]
84%|########3 | 191241/228483 [00:18<00:03, 10488.54it/s]
84%|########4 | 192291/228483 [00:18<00:03, 10471.25it/s]
85%|########4 | 193339/228483 [00:18<00:03, 10410.65it/s]
85%|########5 | 194381/228483 [00:18<00:03, 10381.80it/s]
86%|########5 | 195431/228483 [00:18<00:03, 10414.71it/s]
86%|########5 | 196473/228483 [00:18<00:03, 10390.42it/s]
86%|########6 | 197513/228483 [00:18<00:02, 10365.08it/s]
87%|########6 | 198564/228483 [00:18<00:02, 10402.51it/s]
87%|########7 | 199615/228483 [00:19<00:02, 10433.24it/s]
88%|########7 | 200659/228483 [00:19<00:02, 10433.34it/s]
88%|########8 | 201703/228483 [00:19<00:02, 10426.92it/s]
89%|########8 | 202758/228483 [00:19<00:02, 10462.27it/s]
89%|########9 | 203811/228483 [00:19<00:02, 10481.13it/s]
90%|########9 | 204860/228483 [00:19<00:02, 10470.02it/s]
90%|######### | 205912/228483 [00:19<00:02, 10482.84it/s]
91%|######### | 206963/228483 [00:19<00:02, 10490.44it/s]
91%|#########1| 208013/228483 [00:19<00:01, 10483.80it/s]
92%|#########1| 209062/228483 [00:19<00:01, 10460.75it/s]
92%|#########1| 210109/228483 [00:20<00:01, 10455.25it/s]
92%|#########2| 211160/228483 [00:20<00:01, 10471.26it/s]
93%|#########2| 212208/228483 [00:20<00:01, 10472.83it/s]
93%|#########3| 213256/228483 [00:20<00:01, 10471.06it/s]
94%|#########3| 214304/228483 [00:20<00:01, 10414.80it/s]
94%|#########4| 215346/228483 [00:20<00:01, 10385.46it/s]
95%|#########4| 216393/228483 [00:20<00:01, 10409.00it/s]
95%|#########5| 217434/228483 [00:20<00:01, 10399.46it/s]
96%|#########5| 218474/228483 [00:20<00:00, 10370.61it/s]
96%|#########6| 219521/228483 [00:20<00:00, 10398.03it/s]
97%|#########6| 220571/228483 [00:21<00:00, 10427.55it/s]
97%|#########6| 221616/228483 [00:21<00:00, 10432.03it/s]
97%|#########7| 222660/228483 [00:21<00:00, 10433.81it/s]
98%|#########7| 223714/228483 [00:21<00:00, 10464.49it/s]
98%|#########8| 224766/228483 [00:21<00:00, 10479.90it/s]
99%|#########8| 225815/228483 [00:21<00:00, 10466.00it/s]
99%|#########9| 226865/228483 [00:21<00:00, 10475.96it/s]
100%|#########9| 227918/228483 [00:21<00:00, 10491.36it/s]
100%|##########| 228483/228483 [00:28<00:00, 7949.95it/s]
<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f59de86ef90>
Total running time of the script: ( 1 minutes 20.044 seconds)